NumPy

参考文章：https://zhuanlan.zhihu.com/p/29688927

整体处理流程：

• 初始化参数w、b
• 正向传播，计算损失函数J
• 反向传播，计算dw、db
• 梯度下降优化w、b
• 预测y

1.二分类问题

这一节主要讲了定义数据格式

例：

对于下面这张图片，把它看作64*64个像素点，那么对每个像素点，又可以分为红黄蓝三色：

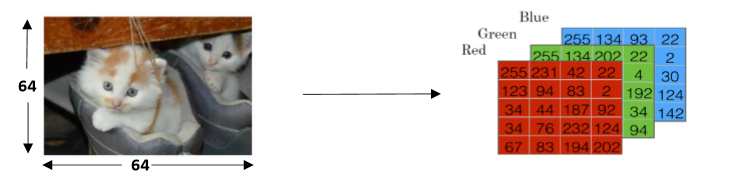
我们可以得出需要的

而y=1/0 可以代表图片中有无猫

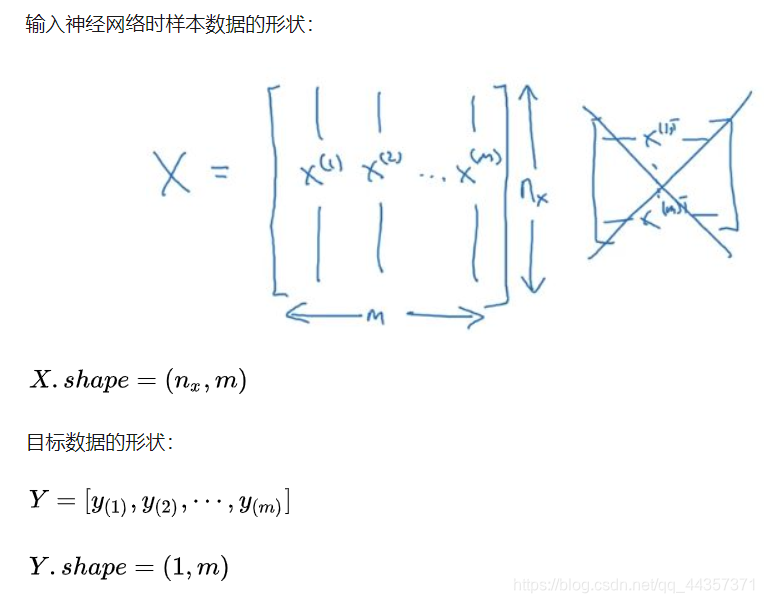
2.logistic regression

上面的 Y^ = [0,1]表示的是一种概率。

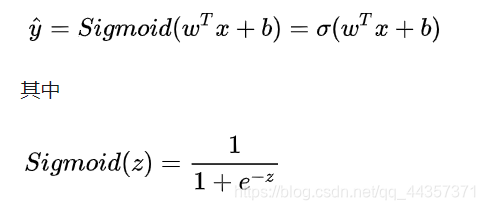
z趋于无穷大，y趋于1；z变小，y变小

控制z，即要获得w、b的值

符号惯例：θo 代表 b；其他的代表w（不同神经）

3.logistic regression损失函数 Loss Function

一般经验来说是用平方错误衡量损失函数

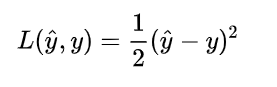
但是，对于logistic regression 来说，一般不适用平方错误来作为Loss Function，这是因为上面的平方错误损失函数一般是非凸函数（non-convex），其在使用梯度下降算法的时候，容易得到局部最优解，而不是全局最优解。因此要选择凸函数。

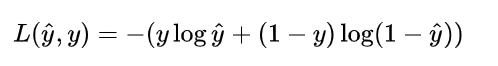
4.梯度下降法

即以梯度下降的方式最小化代价函数cost function,最终得出w、b

每次迭代更新的修正表达式：

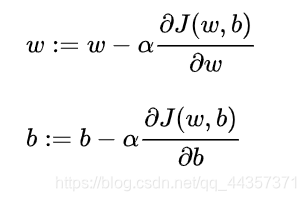
程序中分别用dw、db分别表示上面的偏导部分

5.逻辑回归中的梯度下降法

最后是通过梯度下降法中的修正表达式，得出w1、w2、b的值

6.m个样本的梯度下降

$$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$

$$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$

7.向量化

向量化就是把原始的for循环用矩阵来代替，使用numpy中的矩阵运算直接算出来。

单次迭代梯度下降算法流程：

Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)

w = w - alpha*dw
b = b - alpha*db

8.关于numpy说明

当不确定矩阵的维度时，可以使用assert保证安全

assert(a.shape == (5,1))

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com