NumPy

参考文章：https://zhuanlan.zhihu.com/p/29706138

1、神经网络表示

看着这张浅层神经网络的示意图

第一列为输入层，x1,x2,x3；第二列为隐藏层，第三列为输出层。我们把这个神经网络成为两层神经网络（输入层不计）

我们要注意的是每两层之间的计算和每一层的参数矩阵大小

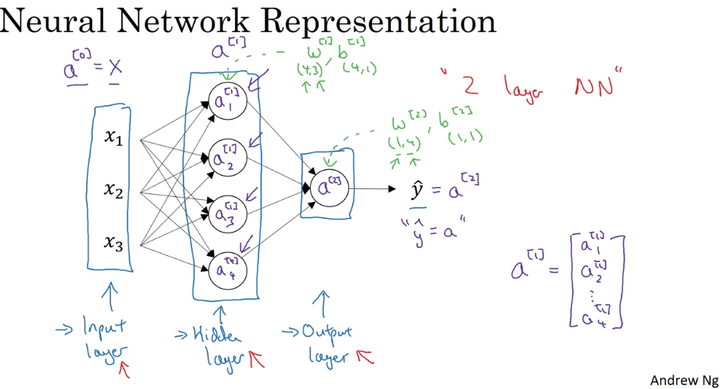
• 输入层和隐藏层

  • w–>(4,3),4代表隐藏层神经元个数，3代表输入层神经元个数
  • b–>(4,1)，4指隐藏层神经元数

• 隐藏层和输出层

  • w–>(1,4),1指输出层，4指隐藏层
  • b–>(1,1),1指输出层

在神经网络中，前一层是输入，后一层作为输出，两层之间，w参数矩阵大小为（N[out], N[in]）, b参数矩阵大小为（N[out], 1）,这里 z = wX + b,神经网络中w[i] = w.T

在logistic regression 中，用（N[in], N[out]）表示参数矩阵大小，公式是 z = w.T***X + b**

2、神经网络的输出

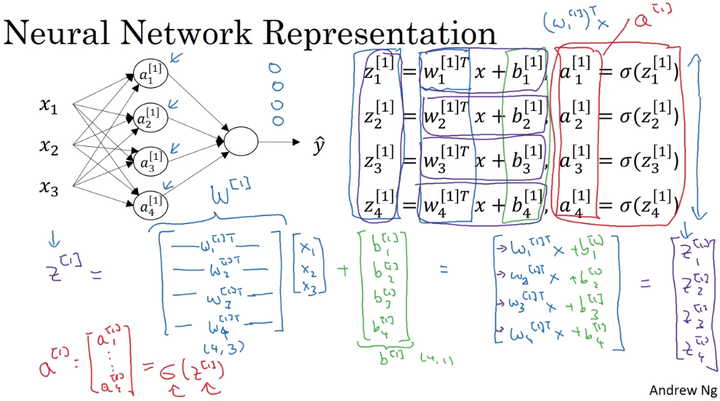
只需要四个公式来控制这个神经网络的输出

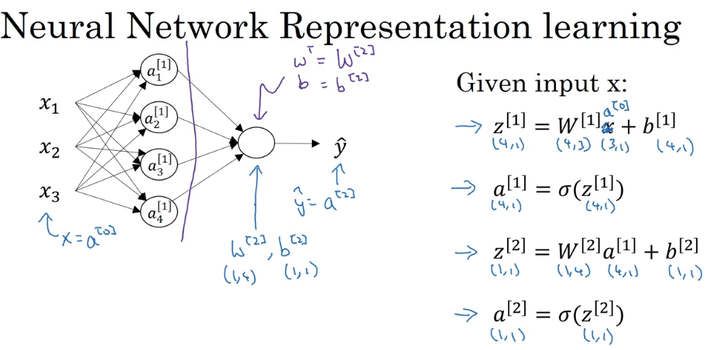
3、向量化

对于每一个神经元x，都需要计算上面的四个公式，如果用for循环，速度十分慢。所以向量化就是使用矩阵来代替for循环，提高效率

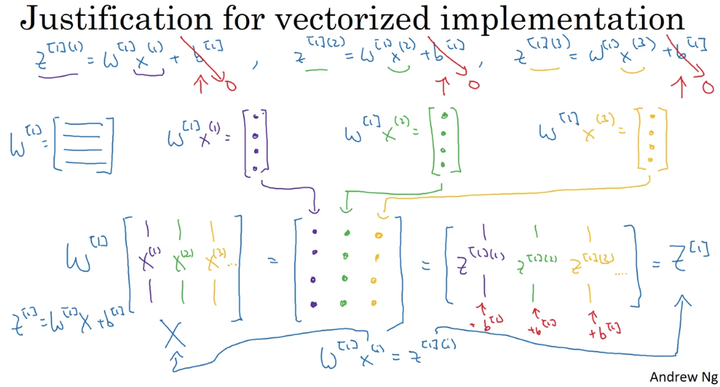
对于m个样本，它的参数矩阵为： （n_x,m）

4、激活函数

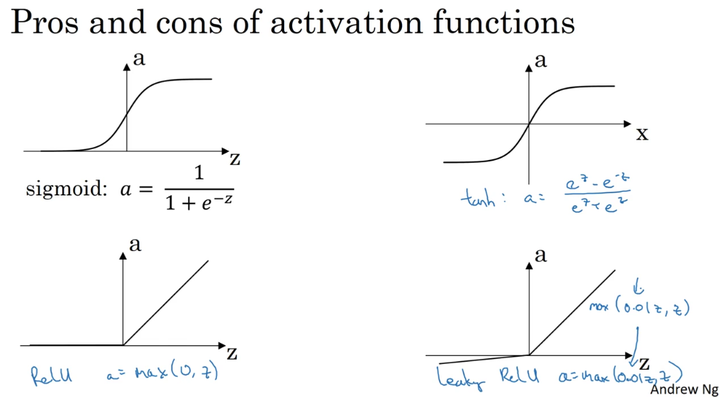
sigmoid函数和tanh函数比较：

• 隐藏层：tanh函数的表现要好于sigmoid函数，因为tanh取值范围为 【-1，1】 ，输出分布在0值的附近，均值为0，从隐藏层到输出层数据起到了归一化（均值为0）的效果。
  输出层：对于二分类任务的输出取值为 【0，1】 ，故一般会选择sigmoid函数。
  然而sigmoid和tanh函数在当 |Z| 很大的时候，梯度会很小，在依据梯度的算法中，更新在后期会变得很慢。在实际应用中，要使 |Z| 尽可能的落在0值附近。

• ReLU弥补了前两者的缺陷，当 Z>0 时，梯度始终为1，从而提高神经网络基于梯度算法的运算速度。然而当 Z<0 时，梯度一直为0，但是实际的运用中，该缺陷的影响不是很大。

• Leaky ReLU保证在 Z<0 的时候，梯度仍然不为0。

在选择激活函数的时候，如果在不知道该选什么的时候就选择ReLU，当然也没有固定答案，要依据实际问题在交叉验证集合中进行验证分析。

5、神经网络的梯度下降

6、随机初始化

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com