NumPy

导包

import numpy as np
import matplotlib.pyplot as plt
from testCases_v2 import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

%matplotlib inline

np.random.seed(1)

加载数据

X, Y = load_planar_dataset()

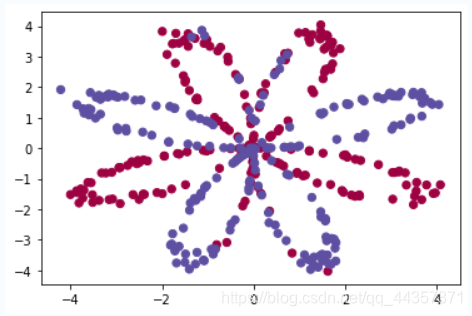
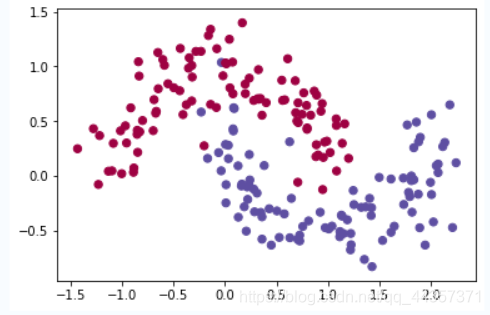
观察数据

plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral);
"""
    关于np.squeeze()
    删除Y中为空的维度
    例如：
    >>> a = e.reshape(1,1,10)
    array([[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]])
    >>> np.squeeze(a)
    array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
"""

'\n    关于np.squeeze()\n    删除Y中为空的维度\n    例如：\n    >>> a = e.reshape(1,1,10)\n    array([[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]])\n    >>> np.squeeze(a)\n    array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])\n'

神经网络每层神经元数

def layer_sizes(X, Y):
    n_x = X.shape[0] #输入层
    n_h = 4 #隐藏层
    n_y = Y.shape[0] #输出层
    return(n_x, n_h, n_y)

初始化参数

def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(2)
    
    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros(shape=(n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros(shape=(n_y, 1))
    
    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                 "b1": b1,
                 "W2": W2,
                 "b2": b2}
    return parameters

向前传播

def forward_propagation(X, parameters):
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    Z1 = np.dot(W1,X)+b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1)+b2
    A2 = sigmoid(Z2)
    
    assert(A2.shape == (1, X.shape[1]))
    cache = {"Z1": Z1,
            "A1": A1,
            "Z2": Z2,
            "A2": A2}
    return A2,cache

计算损失函数

def compute_cost(A2, Y, parameters):
    m = Y.shape[1]
    cost = -1/m * np.sum(Y*np.log(A2)+(1-Y)*np.log(1-A2))
    
    cost = float(np.squeeze(cost))
    assert(isinstance(cost, float))
    return cost

向后传播

def backward_propagation(parameters, cache, X, Y):
    m = X.shape[1]
    
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    
    dZ2 = A2 - Y
    dW2 = 1/m * np.dot(dZ2, A1.T)
    db2 = 1/m * np.sum(dZ2, axis=1, keepdims=True) #按行相加并保持二维特性
    dZ1 = np.dot(W2.T, dZ2) *(1-np.power(A1, 2))
    dW1 = 1/m * np.dot(dZ1, X.T)
    db1 = 1/m * np.sum(dZ1, axis=1, keepdims=True)
    
    grads = {"dW1": dW1,
            "db1": db1,
            "dW2": dW2,
            "db2": db2}
    return grads

更新参数

def update_parameters(parameters, grads, learning_rate = 1.2):
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    
    W1 = W1-learning_rate*dW1
    b1 = b1-learning_rate*db1
    W2 = W2-learning_rate*dW2
    b2 = b2-learning_rate*db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

构造神经网络模型

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    for i in range(0, num_iterations):
        A2, cache = forward_propagation(X, parameters)
        cost = compute_cost(A2, Y, parameters)
        grads = backward_propagation(parameters, cache, X, Y)
        parameters = update_parameters(parameters, grads, learning_rate=0.5)
        
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        
    return parameters

def predict(parameters, X):
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)
    #np.round()函数的作用：对给定的数组进行四舍五入，可以指定精度
    
    return predictions

建立模型

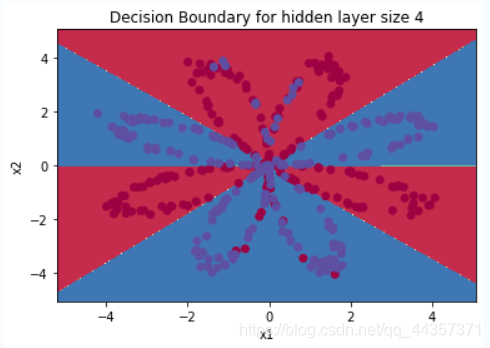
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)

# 画边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.309802
Cost after iteration 2000: 0.292433
Cost after iteration 3000: 0.283349
Cost after iteration 4000: 0.276781
Cost after iteration 5000: 0.263472
Cost after iteration 6000: 0.242044
Cost after iteration 7000: 0.235525
Cost after iteration 8000: 0.231410
Cost after iteration 9000: 0.228464
Accuracy: 90%

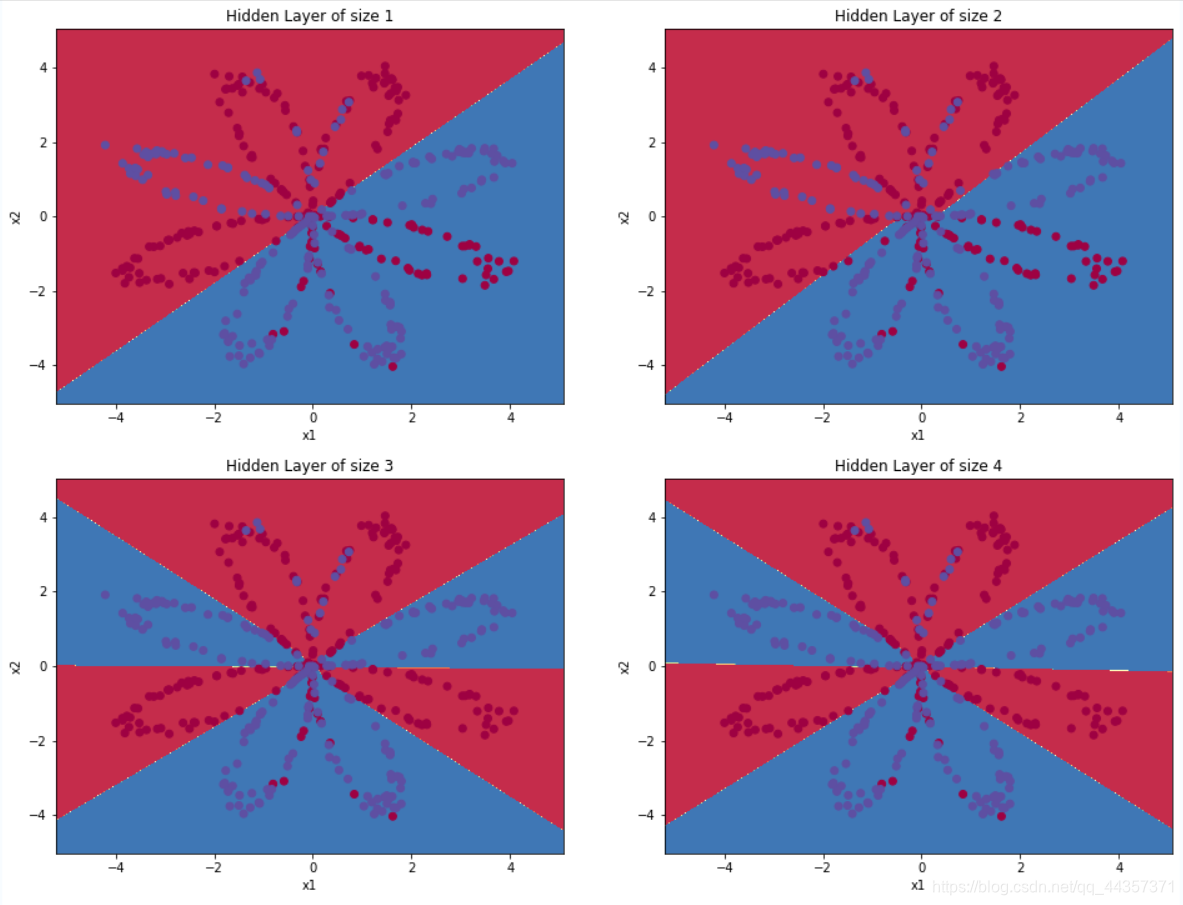
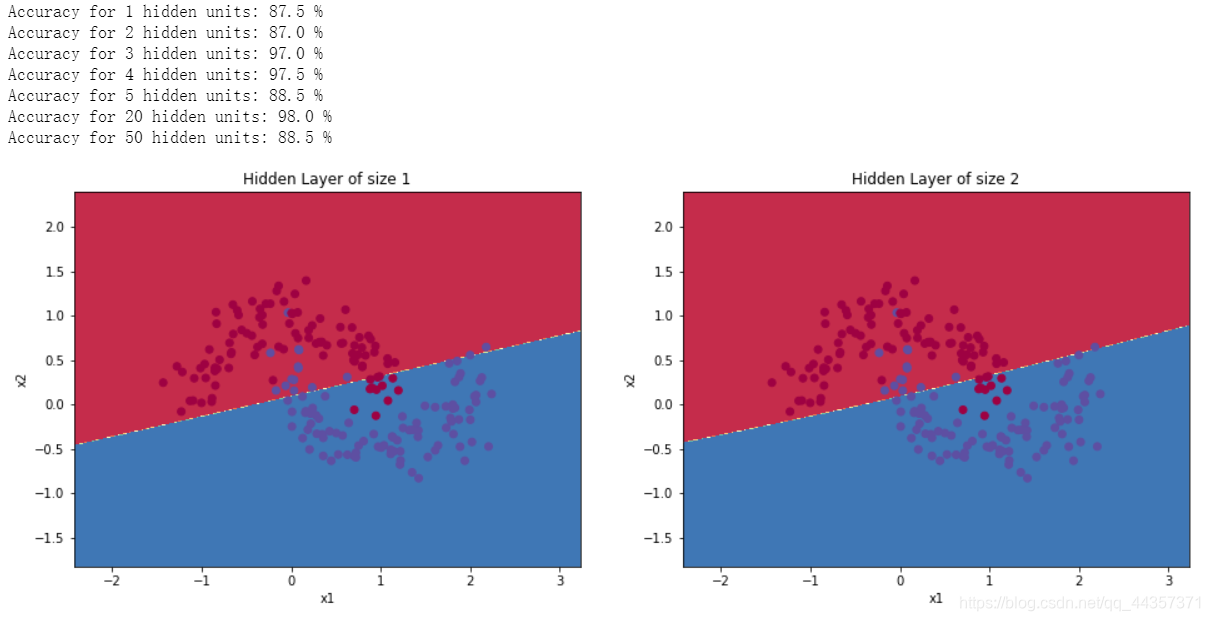
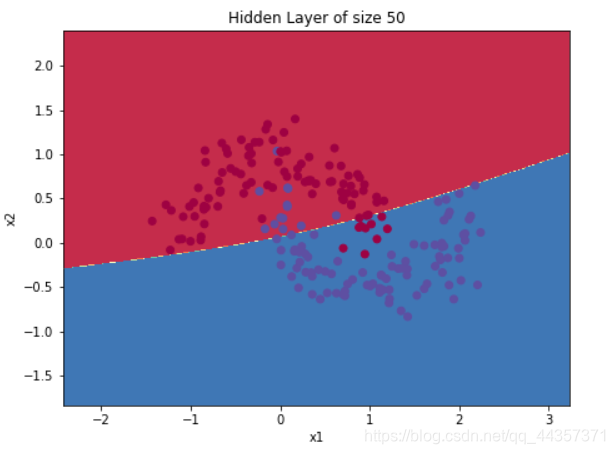
隐藏层数量大小的影响

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

Accuracy for 1 hidden units: 67.25 %
Accuracy for 2 hidden units: 66.5 %
Accuracy for 3 hidden units: 89.25 %
Accuracy for 4 hidden units: 90.0 %
Accuracy for 5 hidden units: 89.75 %
Accuracy for 20 hidden units: 90.0 %
Accuracy for 50 hidden units: 89.75 %

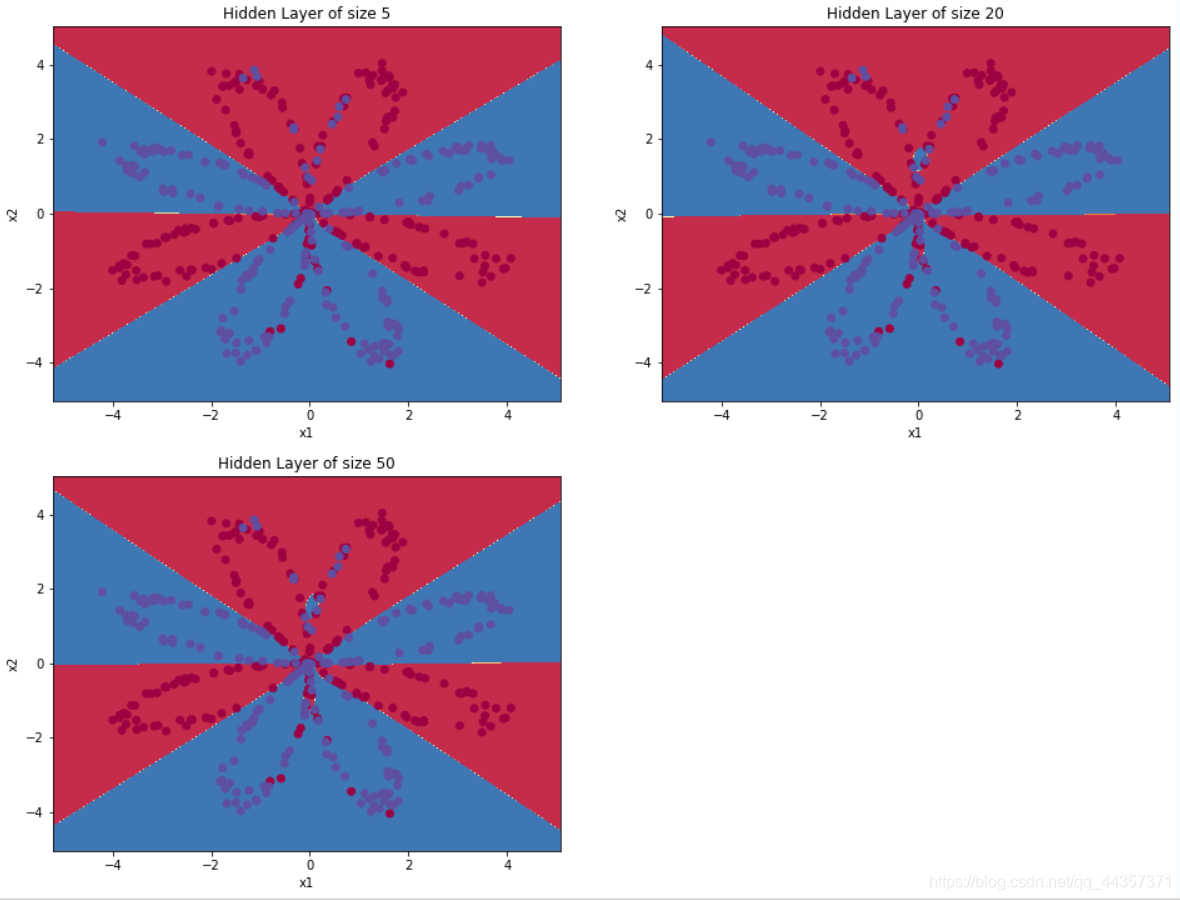
测试其他数据集

# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()

datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

### START CODE HERE ### (choose your dataset)
dataset = "noisy_moons"
### END CODE HERE ###

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

# make blobs binary
if dataset == "blobs":
    Y = Y%2

# Visualize the data
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral);

))

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com