NumPy

导包

import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v4 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2
 
np.random.seed(1)

浅层神经网络参数初始化

def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(1)
    
    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros((n_y, 1))
    
    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                 "b1": b1,
                 "W2": W2,
                 "b2": b2}
    return parameters

L层神经网络参数初始化

def initialize_parameters_deep(layer_dims):
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)
    
    for l in range(1, L): #从1到L-1，不包括L
        parameters['W'+str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*0.01
        parameters['b'+str(l)] = np.zeros((layer_dims[l], 1))
    
        assert(parameters['W'+str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b'+str(l)].shape == (layer_dims[l], 1))
        
    return parameters

实现一个单层正向传播

def linear_forward(A, W, b):
    Z = np.dot(W, A) +b
    
    assert(Z.shape == (W.shape[0], A.shape[1]))
    cache = (A, W, b)
    
    return Z, cache

对一层激活并向前传播（activation_cache存Z，linear_cache存A、W、b）

def linear_activation_forward(A_prev, W, b, activation):
    if activation=="sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
    elif activation=="relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)
        
    assert(A.shape == (W.shape[0], A.shape[1]))
    cache = (linear_cache, activation_cache)
    
    return A, cache

L层正向传播

def L_model_forward(X, parameters):
    caches = []
    A = X
    L = len(parameters)//2 #整数除法，返回一个不大于结果的整数
    
    for l in range(1, L): #前L-1层都用relu，只有最后一层用sigmoid
        A_prev = A
        A,cache = linear_activation_forward(A_prev, parameters['W'+str(l)], parameters['b'+str(l)], "relu")
        caches.append(cache)
    
    AL, cache = linear_activation_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], "sigmoid")
    caches.append(cache)
    
    assert(AL.shape == (1,X.shape[1]))
    
    return AL, caches

损失函数

def compute_cost(AL, Y):
    m = Y.shape[1]
    cost = -1/m*np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))
    
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    return cost

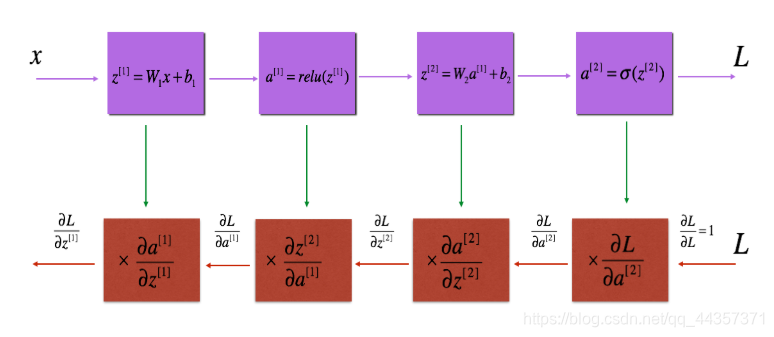
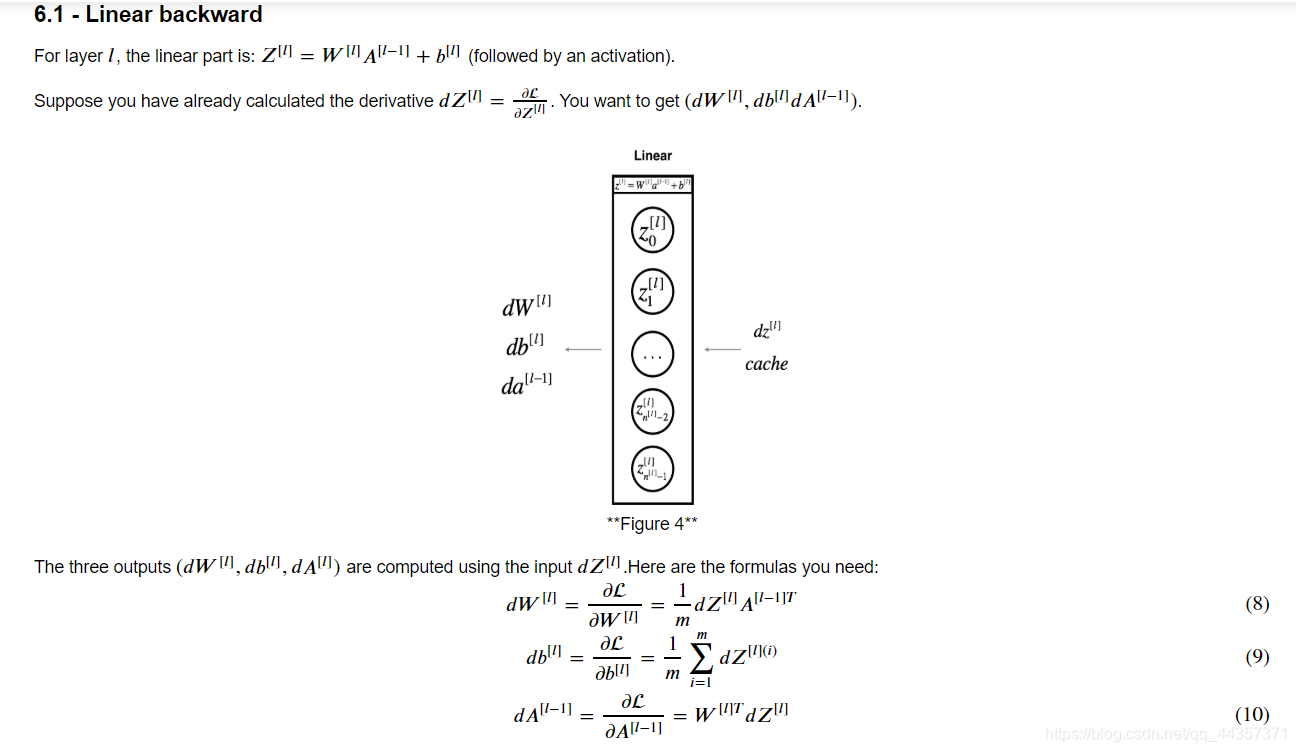
单层向后传播

def linear_backward(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]
    
    dW = 1/m * np.dot(dZ, A_prev.T)
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    assert(dW.shape == W.shape)
    assert(db.shape == b.shape)
    assert(dA_prev.shape == A_prev.shape)
    
    return dA_prev, dW, db

对单层激活并向后传播

def linear_activation_backward(dA, cache, activation):
    linear_cache, activation_cache = cache
    
    if activation=="relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation=="sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        
    return dA_prev, dW, db

L层向后传播

def L_model_backward(AL, Y, caches):
    grads={}
    L = len(caches)
    m = AL.shape[1]
    Y = Y.reshape(AL.shape)
    
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    
    current_cache = caches[L-1]
    grads["dA"+str(L-1)], grads["dW"+str(L)], grads["db"+str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
    
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        # Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, "relu")
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
        
    return grads

更新参数

def update_parameters(parameters, grads, learning_rate):
    L = len(parameters) // 2  # 神经网络的层数
    
    for l in range(L): #从0到L-1
        parameters["W"+str(l+1)] = parameters["W"+str(l+1)]-learning_rate*grads["dW"+str(l+1)]
        parameters["b"+str(l+1)] = parameters["b"+str(l+1)]-learning_rate*grads["db"+str(l+1)]
    return parameters

parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)

print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))

W1 = [[-0.59562069 -0.09991781 -2.14584584  1.82662008]
 [-1.76569676 -0.80627147  0.51115557 -1.18258802]
 [-1.0535704  -0.86128581  0.68284052  2.20374577]]
b1 = [[-0.04659241]
 [-1.28888275]
 [ 0.53405496]]
W2 = [[-0.55569196  0.0354055   1.32964895]]
b2 = [[-0.84610769]]

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com