编程作业——优化Optimization

DeepLearning/ 02改善深层神经网络 神经网络
创建时间:
字数:1.2k 阅读: 评论:
  1. Gradient Descent
  2. Mini-Batch Gradient descent
  3. Momentum
  4. Adam
  5. Mini-batch Gradient descent
  6. Mini-batch gradient descent with momentum
  7. Mini-batch with Adam mode
  8. Summary

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets

from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

Gradient Descent

1
2
3
4
5
6
7
8
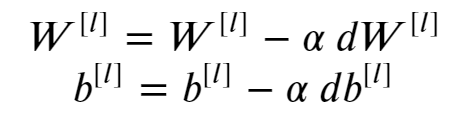
def update_parameters_with_gd(parameters, grads, learning_rate):
    L = len(parameters) // 2
    
    for l in range(L):
        parameters["W"+str(l+1)] = parameters["W"+str(l+1)]-learning_rate*grads["dW"+str(l+1)]
        parameters["b"+str(l+1)] = parameters["b"+str(l+1)]-learning_rate*grads["db"+str(l+1)]
        
    return parameters

Mini-Batch Gradient descent

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
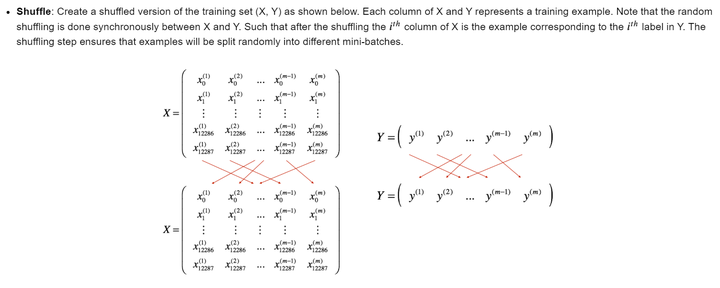
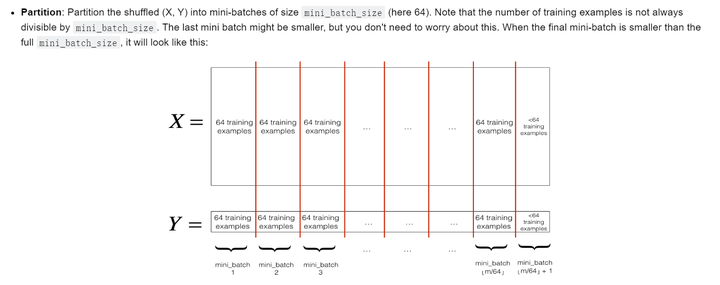
23
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []
    
    permutation = list(np.random.permutation(m)) #对m个数随机排列
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1,m))
    
    num_complete_minibatches = math.floor(m/mini_batch_size) # 向上取整
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, 0:mini_batch_size]
        mini_batch_Y = shuffled_Y[:, 0:mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
        
    if m%mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, mini_batch_size:2*mini_batch_size]
        mini_batch_Y = shuffled_Y[:, mini_batch_size:2*mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    return mini_batches

Momentum

1
2
3
4
5
6
7
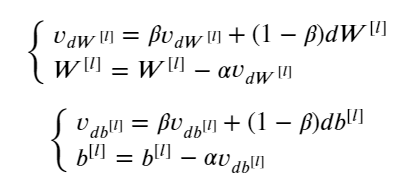
8
def initialize_velocity(parameters):
    L = len(parameters)//2
    v = {}
    
    for l in range(L):
        v["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
        v["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
    return v
1
2
3
4
5
6
7
8
9
10
11
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    L = len(parameters)//2
    
    for l in range(L):
        v["dW"+str(l+1)] = beta*v["dW"+str(l+1)]+(1-beta)*grads["dW"+str(l+1)]
        v["db"+str(l+1)] = beta*v["db"+str(l+1)]+(1-beta)*grads["db"+str(l+1)]
        
        parameters["W"+str(l+1)] = parameters["W"+str(l+1)]-learning_rate*v["dW"+str(l+1)]
        parameters["b"+str(l+1)] = parameters["b"+str(l+1)]-learning_rate*v["db"+str(l+1)]
        
    return parameters, v

Adam

1
2
3
4
5
6
7
8
9
10
11
12
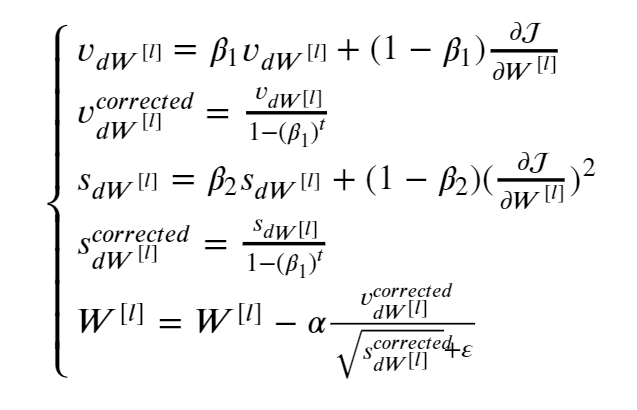
def initialize_adam(parameters):
    L = len(parameters)//2
    v = {}
    s = {}
    
    for l in range(L):
        v["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
        v["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
        s["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
        s["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
        
    return v, s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01, beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
    L = len(parameters)//2
    v_corrected = {}
    s_corrected = {}
    
    for l in range(L):
        v["dW"+str(l+1)] = beta1 * v["dW"+str(l+1)] + (1-beta1)*grads["dW"+str(l+1)]
        v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1)*grads["db"+str(l+1)]
        
        s["dW"+str(l+1)] = beta2 * s["dW"+str(l+1)] + (1-beta2)*grads["dW"+str(l+1)]*grads["dW"+str(l+1)]
        s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1-beta2)*np.power(grads["db"+str(l+1)], 2)
        
        v_corrected["dW"+str(l+1)] = v["dW"+str(l+1)]/(1-np.power(beta1, t))
        v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-np.power(beta1, t))
        
        s_corrected["dW"+str(l+1)] = s["dW"+str(l+1)]/(1-np.power(beta1, t))
        s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-np.power(beta2, t))
        
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)
        
    return parameters, v, s
1
train_X, train_Y = load_dataset()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
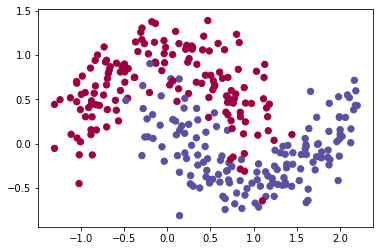
60
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
          beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8, num_epochs = 10000, print_cost = True):
   
    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10
    
    parameters = initialize_parameters(layers_dims)

    if optimizer == "gd":
        pass # no initialization required for gradient descent
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)
    
    for i in range(num_epochs):
        
        seed = seed + 1
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        for minibatch in minibatches:

            # Select a minibatch
            (minibatch_X, minibatch_Y) = minibatch

            # Forward propagation
            a3, caches = forward_propagation(minibatch_X, parameters)

            # Compute cost
            cost = compute_cost(a3, minibatch_Y)

            # Backward propagation
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)

            # Update parameters
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
            elif optimizer == "adam":
                t = t + 1 # Adam counter
                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
                                                               t, learning_rate, beta1, beta2,  epsilon)
        
        # Print the cost every 1000 epoch
        if print_cost and i % 1000 == 0:
            print ("Cost after epoch %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
                
    # plot the cost
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters

Mini-batch Gradient descent

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Cost after epoch 0: 0.708983
Cost after epoch 1000: 0.659841
Cost after epoch 2000: 0.628205
Cost after epoch 3000: 0.571343
Cost after epoch 4000: 0.593195
Cost after epoch 5000: 0.503812
Cost after epoch 6000: 0.507677
Cost after epoch 7000: 0.494559
Cost after epoch 8000: 0.459184
Cost after epoch 9000: 0.399013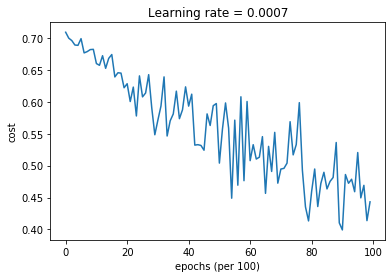

Accuracy: 0.7966666666666666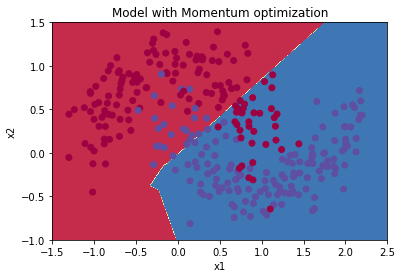

Mini-batch gradient descent with momentum

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Cost after epoch 0: 0.709029
Cost after epoch 1000: 0.659953
Cost after epoch 2000: 0.628344
Cost after epoch 3000: 0.571453
Cost after epoch 4000: 0.593252
Cost after epoch 5000: 0.503935
Cost after epoch 6000: 0.507794
Cost after epoch 7000: 0.494631
Cost after epoch 8000: 0.459387
Cost after epoch 9000: 0.399227

Accuracy: 0.7966666666666666

Mini-batch with Adam mode

1
2
3
4
5
6
7
8
9
10
11
12
13
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Cost after epoch 0: 0.700736
Cost after epoch 1000: 0.171262
Cost after epoch 2000: 0.119976
Cost after epoch 3000: 0.258917
Cost after epoch 4000: 0.079703
Cost after epoch 5000: 0.119927
Cost after epoch 6000: 0.150617
Cost after epoch 7000: 0.131514
Cost after epoch 8000: 0.159743
Cost after epoch 9000: 0.057505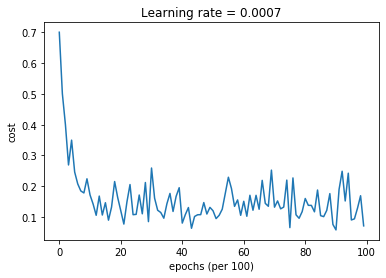

Accuracy: 0.93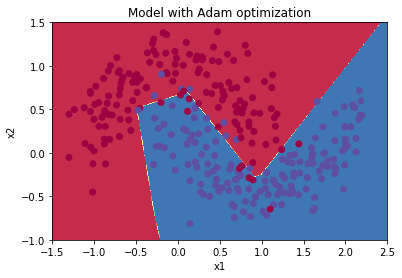

Summary

**optimization method** **accuracy** **cost shape**
Gradient descent 79.7% oscillations
Momentum 79.7% oscillations
Adam 94% smoother
转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com

赏

文章标题:编程作业——优化Optimization

文章字数:1.2k

本文作者:runze

发布时间:2020-02-18, 10:28:29

最后更新:2020-02-23, 08:31:01

原始链接:http://yoursite.com/2020/02/18/%E5%90%B4%E6%81%A9%E8%BE%BE%20%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/02%E6%94%B9%E5%96%84%E6%B7%B1%E5%B1%82%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%EF%BC%9A%E8%B6%85%E5%8F%82%E6%95%B0%E8%B0%83%E8%AF%95%E3%80%81%E6%AD%A3%E5%88%99%E5%8C%96%E4%BB%A5%E5%8F%8A%E4%BC%98%E5%8C%96/%E7%BC%96%E7%A8%8B%E4%BD%9C%E4%B8%9A%E2%80%94%E2%80%94%E4%BC%98%E5%8C%96Optimization/

版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

©2020 runze

Built with Hexo and 3-hexo theme

目录
×

喜欢就点赞,疼爱就打赏