NumPy

参考文章：https://zhuanlan.zhihu.com/p/30800318

1、计算机视觉

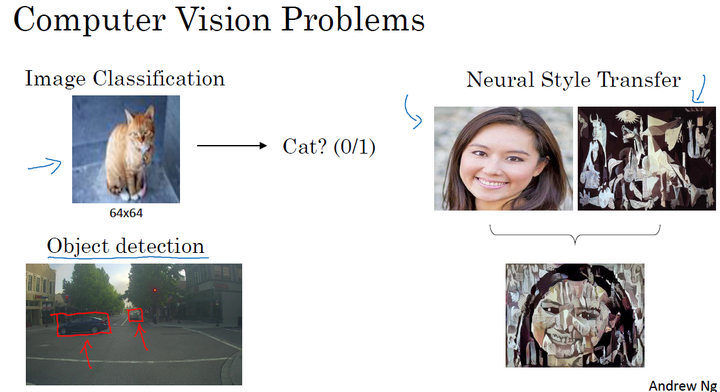
对于小尺寸的图片，我们通过神经网络可以解决。但是当尺寸非常大，如果仍使用神经网络，则需要计算很多参数，这时候神经网络就不再适用。

卷积神经网络在计算机视觉问题上是一个非常好的网络结构。

2、边缘检测示例

下面的图中，分别通过垂直边缘检测和水平边缘检测得到不同的结果：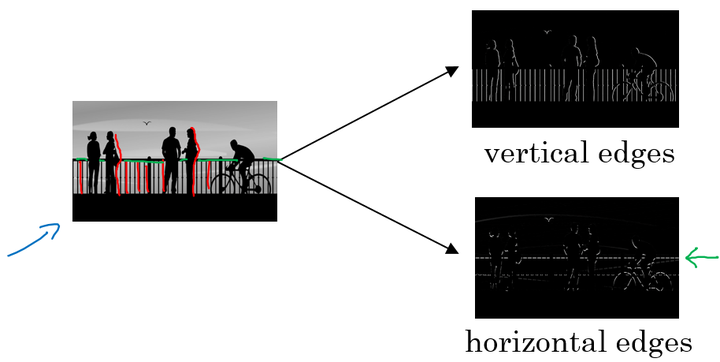

垂直边缘检测

对于一个 6X6 大小的图片，和一个 3X3 大小的filter卷积核，进行卷积运算，以“ * ”表示，图片和垂直边缘检测器分别如左和中矩阵所示：

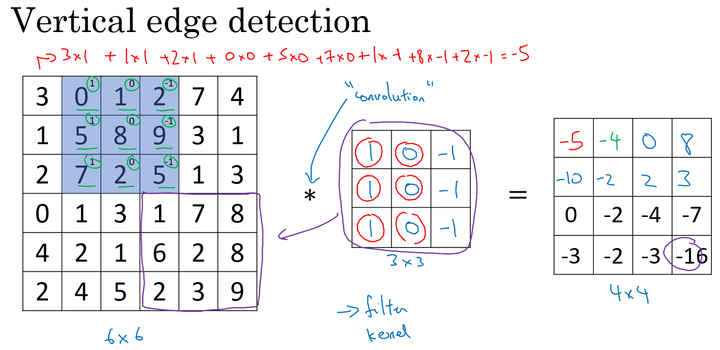
filter 不断地和其大小相同的部分做对应元素的乘法运算并求和，最终得到的数字相当于新图片的一个像素值，如右矩阵所示，最终得到一个 4X4 大小的图片。

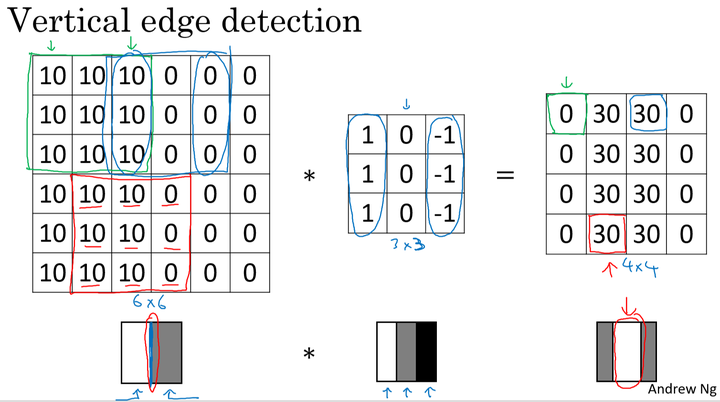
边缘检测的原理

以一个有一条垂直边缘线的简单图片来说明。通过垂直边缘 filter 我们得到的最终结果图片可以明显地将边缘和非边缘区分出来：

多种边缘检测

• 垂直和水平边缘检测

• 更复杂的 filter

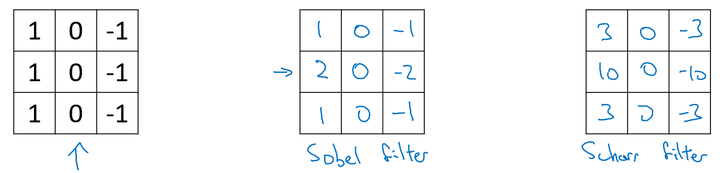
对于复杂的图片，我们可以直接将 filter 中的数字直接看作是需要学习的参数，其可以学习到对于图片检测相比上面filter更好的更复杂的 filter ，如相对于水平和垂直检测器，我们训练的 filter 参数也许可以知道不同角度的边缘。

通过卷积运算，在卷积神经网络中通过反向传播算法，可以学习到相应于目标结果的 filter，将其应用于整个图片，输出其提取到的所有有用的特征。

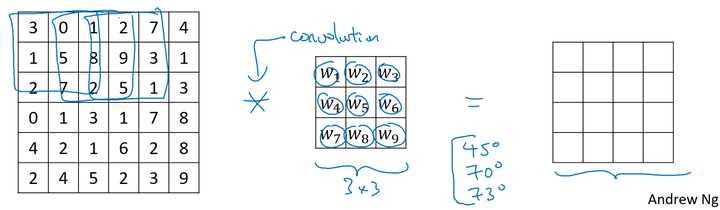
卷积和互相关：

在数学定义上，矩阵的卷积（convolution）操作为首先将卷积核同时在水平和垂直方向上进行翻转，构成一个卷积核的镜像，然后使用该镜像再和前面的矩阵进行移动相乘求和操作。如下面例子所示：

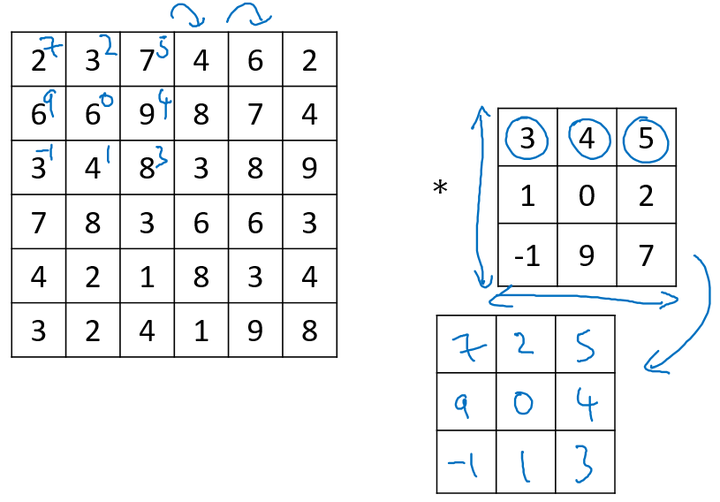
在深度学习中，我们称为的卷积运算实则没有卷积核变换为镜像的这一步操作，因为在权重学习的角度，变换是没有必要的。深度学习的卷积操作在数学上准确度来说称为互相关（cross-correlation）。

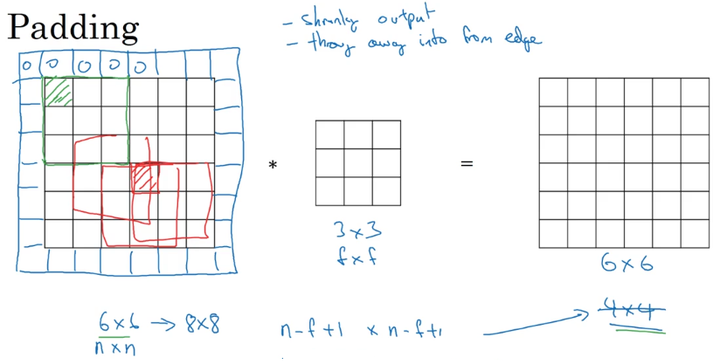
3、Padding

没有Padding的缺点：

• 每次卷积操作，图片会缩小；
  就前面的例子来说， 6X6 大小的图片，经过 3X3 大小的 filter，缩小成了 4X4 大小图片： n X n –> (n-f+1)X(n-f+1)

• 角落和边缘位置的像素进行卷积运算的次数少，可能会丢失有用信息。

其中，n 表示图片的长或宽的大小，f 表示filter的长或宽的大小。

加Padding：

为了解决上面的两个缺点，我们在进行卷积运算前为图片加padding，包围角落和边缘的像素，使得通过filter的卷积运算后，图片大小不变，也不会丢失角落和边沿的信息。

以p表示 Padding 的值，则输入 nXn 大小的图片，最终得到的图片大小为 (n+2p-f+1)X(n+2p-f+1) ，为使图片大小保持不变，需根据filter的大小调整p的值。

Valid / Same 卷积：

Valid：no padding；（ nXn –> (n-f+1)X(n-f+1)）
Same：padding，输出与输入图片大小相同，（ p=(f-1)/2 ）。在计算机视觉中，一般来说padding的值为奇数（因为filter一般为奇数）

4、卷积步长（stride）

卷积的步长是构建卷积神经网络的一个基本的操作。

如前面的例子中，我们使用的 stride=1，每次的卷积运算以1个步长进行移动。下面是 stride=2 时对图片进行卷积的结果：

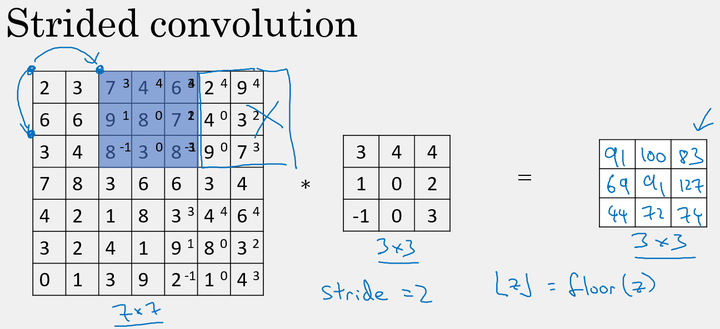
以s表示stride的大小，那么在进行卷积运算后，图片的变化为：

注意，在当 padding ≠ 1 时，若移动的窗口落在图片外面，则不要再进行相乘的操作，丢弃边缘的数值信息，所以输出图片的最终维度为向下取整。

5、立体卷积

卷积核的通道数：

对于灰色图像中，卷积核和图像均是二维的。而应用于彩色图像中，因为图片有R、G、B三个颜色通道，所以此时的卷积核应为三维卷积核。

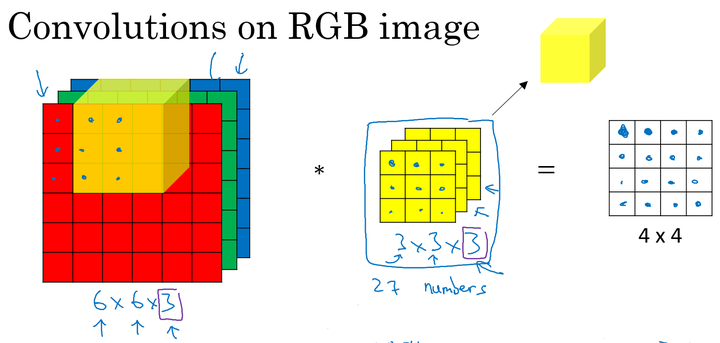
卷积核的第三个维度需要与进行卷积运算的图片的通道数相同。

多卷积核：

单个卷积核应用于图片时，提取图片特定的特征，不同的卷积核提取不同的特征。如两个大小均为 3X3X3 的卷积核分别提取图片的垂直边缘和水平边缘。

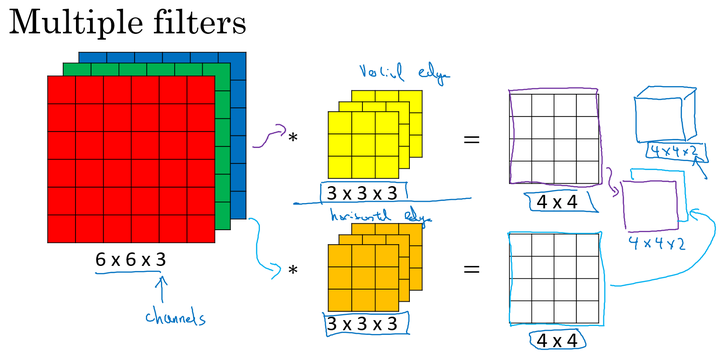
由图可知，最终提取到彩色图片的垂直特征图和水平特征图，得到有2个通道的 4X4 大小的特征图片。

总结

其中：nc表示通道数量，nc’表示下层通道数，同时等于本层卷积核个数

6、单层卷积网络

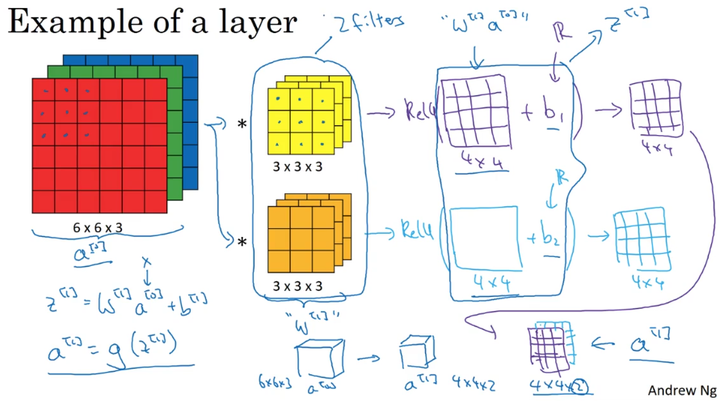
例如：我们有十个 3X3X3 的卷积核fliter，则共有参数个数为：

（3x3x3+1）x 10 = 280 (其中，加一是加上偏置b)

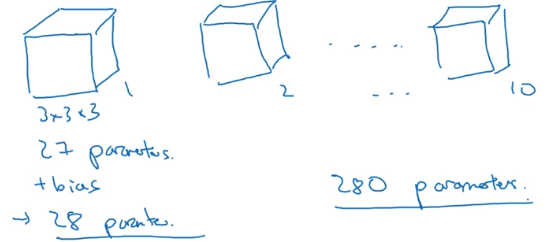
无论图片大小是多少，该例子中的卷积层参数个数一直都是280个，相对于普通的神经网络，卷积神经网络的参数个数要少很多。

7、简单卷积网络示例

上图的过程就是卷积层。

卷积神经网络的类型：

• 卷积层（Convolution）Conv；
• 池化层（Pooling）Pool；
• 全连接层（Fully Connected）FC

8、池化层

除了卷积层，卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高
所提取特征的鲁棒性。

最大池化（max pooling）

最大池化是对前一层得到的特征图进行池化减小，仅由当前小区域内的最大值来代表最终池化后的值。

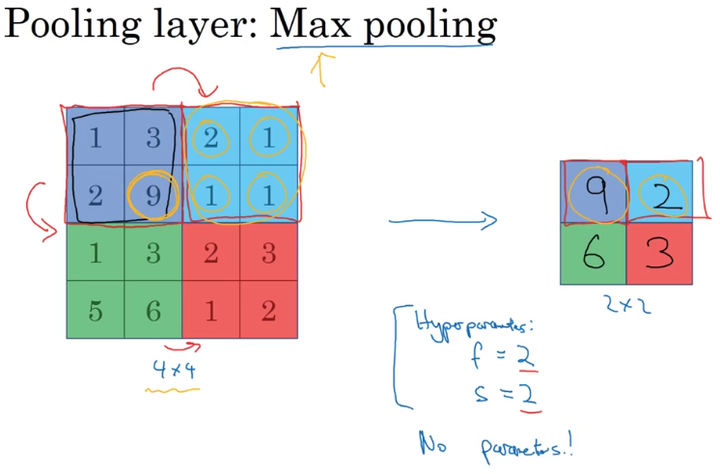
池化前： n×n

池化后：

平均池化（Average pooling）

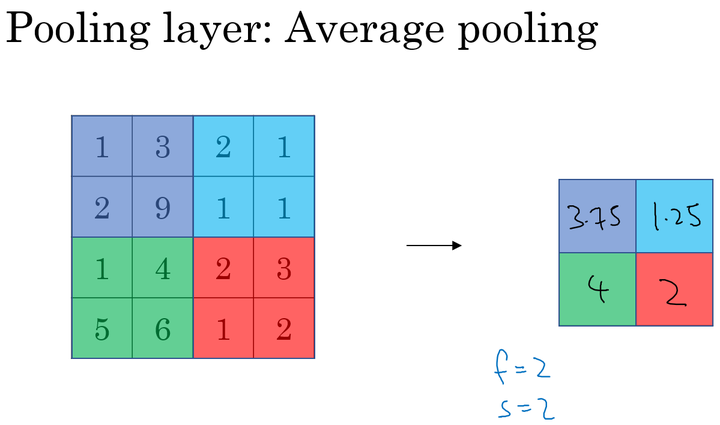
池化层没有需要学习的参数

9、卷积神经网络示例

例：

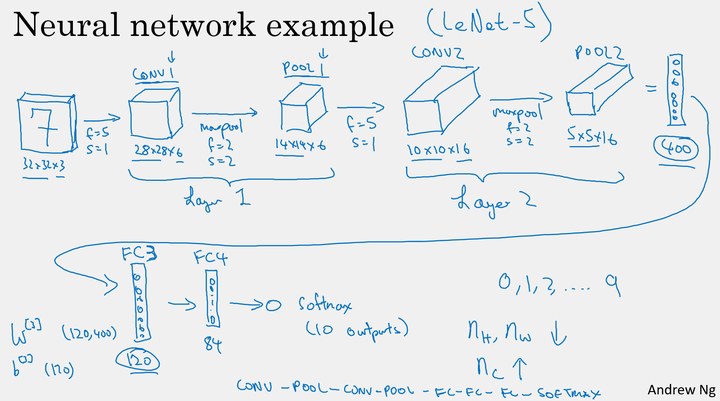
构建深度卷积的模式：

• 随着网络的深入，提取的特征图片大小将会逐渐减小，但同时通道数量应随之增加；
• Conv——Pool——Conv——Pool——Fc——Fc——Fc——softmax。

卷积神经网络的参数：

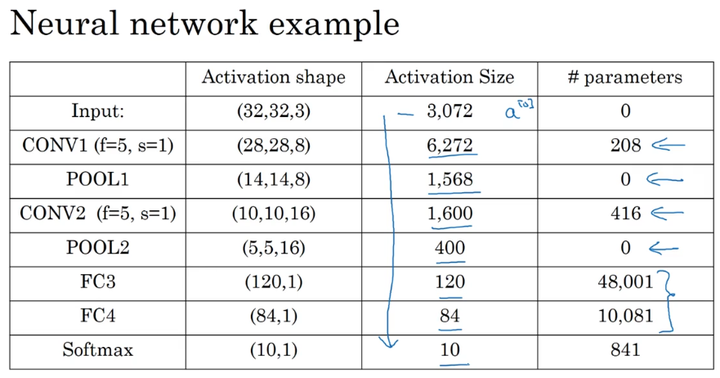
根据上表我们可以看出，对于卷积卷积神经网络的参数：

• 在卷积层，仅有少量的参数；
• 在池化层，没有参数；
• 在全连接层，存在大量的参数。

10、为什么使用卷积

参数少的优势：

与普通的全连接神经网络相比，卷积神经网络的参数更少。如图中的例子，卷积神经网络仅有 6x(5x5+1) = 156 个参数，而普通的全连接网络有 3072x4704=14M 个参数。

• 参数共享：一个特征检测器（filter）对图片的一部分有用的同时也有可能对图片的另外一部分有用。
• 连接的稀疏性：在每一层中，每个输出值只取决于少量的输入。

训练卷积神经网络：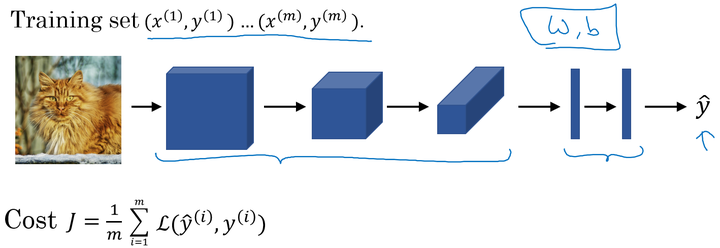

我们将训练集输入到卷积神经网络中，对网络进行训练。利用梯度下降（Adam、momentum等优化算法）最小化代价函数来寻找网络的最优参数。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 2470290795@qq.com